Earth Curvature for Highpointers *

Account of surface curvature is presented at two levels of accuracy. The first level assumes Earth's surface is a perfect sphere.
The second level accounts nike shox monster for its true form which is better approximated by an oblate spheroid.

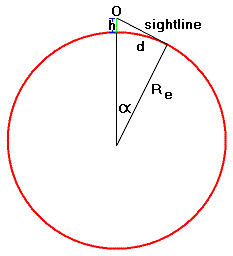
Figure 1

h   =   (sec α - 1) Re

(1a)

such that

α   =   sec-1 (1 + h / Re)

(2)

where α is the geocentric angle subtended by d.

Using d = α R_e,

d   =   Re * sec-1 (1 + h / Re)

(3a)

Equation (3a) is exact for all observer heights h.

For all mountains we have h << R_e, allowing for a valid approximation by noting

sec x   ≈   1 + ½ x2

x << 1

(4).

We obtain

d   ≈   (2 Re h)½.

(3b)

Using 3,959 statute miles for R_e (a good mean value as shown later),

1. The arcsecant function is numerically unstable at small arguments since its derivative
    approaches infinity there. Therefore in the algorithm we replace it with the arctangent function,
    recalling the trigonometric identity sec² x = 1 + tan² x. Defining β = h / R_e we obtain d = tan^-1 ( [β (2 + β)]^1/2 ) R_e.

Hand Level Elevation Correction

The geometric apparatus for computing horizon distance may equally be used to find a hand level elevation correction. When one sights to a nearby summit the apparent horizon lies above a summit of identical height to the observer - a direct result of Earth surface curvature.

Equation (1a) is the desired elevation correction. Application of Equation (4) yields a valid approximation for the short distances relevant to hand leveling,

h   ≈   d2 / (2 Re) .

(1b)

Equation (1b) is also trivally obtained from Equation (3b).

The elevation correction magnitude rises as the distance squared.
Again using a 3,959 mile Earth radius we have

Thus at one mile an object 8 inches higher than the sight leveler appears to be at the same elevation.
Similarly, at one-half mile an object at his elevation appears to be 2 inches lower.

Equation (1c) is valid only for the short distances encountered with hand leveling. For larger observer to horizon distances (such as encountered with high altitude aircraft and satellites) the more robust formula (1a) is required. This calculator provides valid results for all observer to object distances out to the theoretical maximum of one-quarter Earth's circumference (some 6,218 miles).

Type an observation distance in the left textfield, in miles, to calculate the corresponding elevation correction in feet.

The above formulations may incorporate altitude above sea level v through replacement of R_e by R_e + v. Thus if the observer is at 17,000 feet and the distant horizon is generally at 5,000 feet he should use h = 12,000 feet and R_e = 3,960 miles.

The curvature of arcs along Earth's surface is considerably more involved upon account of its ellipsoidal shape. We desire the instantaneous, local curvature of that unique geodesic passing through the observer and heading towards the distant object.²

A great simplication is afforded in that we are only concerned with the geodesic's local curvature at the observer, so obviating decidedly tedious calculations that cannot be solved analytically (i.e. in "closed-form" and requiring numerical methods).

We therefore may replace the geodesic with the corresponding great elliptic arc, one that lies in a plane passing through Earth's center and that cuts the observer's position at an angle φ with his meridional plane.^3,4 When he sights at a true bearing of φ the observable distance is determined by that particular great elliptic arc's local radius of curvature.⁵

Throughout this section terms that contribute in higher order than 1/e² will be neglected where e² is the squared first eccentricity defined by Equation [9] below. This enables analytical results to be presented, and is a sufficiently accurate formulation because terms of higher order only contribute for distances larger than of concern to highpointers.

2. A geodesic is the shortest path on any surface. For a plane it is a straight line and for the sphere a great circle.
    See mathworld.wolfram.com for a modern formulation and a modification of the original formulation by Bessel in the 1820s.

Radius of Curvature Derivation - Meridional Arcs

We consider a plane slicing Earth's surface such that their intersection is the great elliptic arc.
For a plane curve defined parametrically as γ(t) = (x(t), y(t)) we have the curvature

κ   =   |x'y" - y'x"| / (x'2 + y'2)3/2 ,

(5)

where the primes indicate differentiation with respect to parameter t.
The radius of curvature, henceforth r, is the multiplicative inverse of κ.

Using standard notation, the equatorial radius is denoted a, the polar radius b.

We first derive the simpler case of an ellipse lying in any meridional plane (hence including both poles),
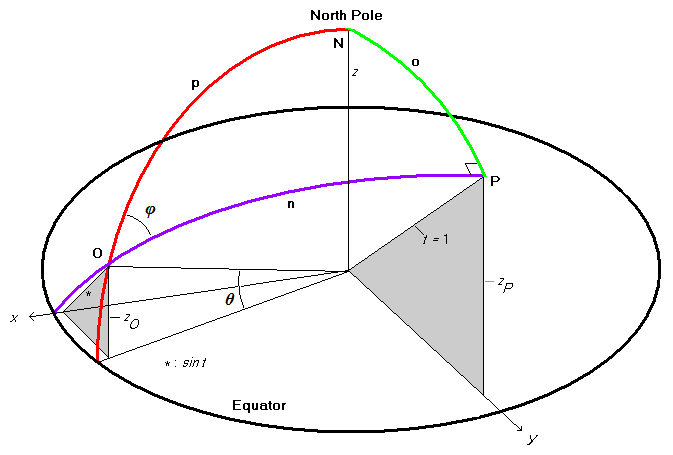
partially shown in Figure 2 as the red arc. For it we have the parametric equations

x = a cos t     (6a)

y = b sin t     (6b)

Substitution of these equations into Equation (5) yields

r   =   ( a2 sin2 t + b2 cos2 t)3/2 / ab .

(7a)

Figure 2

For meridional arcs parameter t equals the parametric latitude θ, also called the reduced latitude.
θ is related to the well-known geographic latitude (or geodetic latitude) θ_g by

tan θ   =   (b/a) tan θg .

(8)

Therefore θ is slightly less than θ_g except at the Equator and poles where they coincide.

Equation (7a) is not particularly enlightening and is recast using the squared eccentricity,

e2   =   1 - (b/a)2     << 1

(9)

to obtain

r   =   (a2/b) / (1 - e2 cos2 t)3/2 .

(7b)

Using e² << 1 and a/b ≈ 1 + ½ e² we have after some algebra

r   ≈   a ( 1 + ½ e2 [1 - 3 cos2 t] ).

(7c)

Thus viewing due north or south the radius of curvature is roughly linear in a small magnitude term proportional to the latitude's squared cosine. The maximal radius of curvature is at either pole with r ≈ a (1 + ½ e²); the minimal radius at the Equator with r ≈ a (1 - e²).

For the WGS84 ellipsoid e² = 0.00669437999013, roughly 1 part in 150. Hence at either pole the radius of curvature for any heading is roughly 1 part in 300 greater than the equatorial radius (every direction being due north or due south!); and the radius of curvature for a north-south sighting at the equator is roughly 1 part in 150 less than the equatorial radius. It will be seen that these values are, in fact, the maximal and minimal values r assumes for all possible observer sight angles.

Radius of Curvature Derivation - General Case

We now consider the general case of a great elliptic arc passing through the observer at an arbitrary angle with respect to his meridian and shown in Figure 2 as the violet arc. Point O is the observer's location. The above considerations correspond to the special case of φ = 0°, i.e. the arc's bearing is exactly 0 (or 180) degrees. With reference to Figure 2 we have from spherical trigonometry

sin o = sin φ sin p	(10a)
= sin φ cos θ	(10b)

where θ is the observer's parametric latitude.⁶

In Figure 2, 90° - lime green arc o gives the maximal excursion of our great elliptic arc from the Equator. Its semi-minor radius r_min is the distance to Earth's center of the corresponding point at right angle P,

r_min   =   a (1 - e2 sin2 [π/2 - o])½     (11a)

=   a (1 - e2 cos2 o)½               (11b).

and provides an "effective b" from which one computes a radius of curvature anywhere along the arc using Equation (7a).
The semi-major radius for such a computation is, of course, just the equatorial radius a.

To proceed we require the value of parameter t along this great elliptic arc corresponding to the observer's location O.

At point P parameter t assumes its maximal value of 1.0 as shown in the figure.
Noting the pair of gray similar right triangles with angles π/2 - φ,

sin t / 1   =   zO / zP             (12)

z_P is the vertical coordinate of point P. Furthermore arc o is the co-latitude of P.
Thus z_P = sin (π/2 - o) = cos o apart from a scaling factor. Hence from Equation (12) we obtain

sin t       =   sin θ / cos o     (13).

Manipulation of Equations (10b) and (13) provides expressions for sin² t and cos² t
in terms of observer parametric latitude θ and sighting angle φ.

sin2 t   =               sin2 θ / (1 - sin2 φ cos2 θ)     (14)

cos2 t   =   cos2 θ cos2 φ / (1 - sin2 φ cos2 θ)     (15)

Substitution of these expressions and r_min from Equation (11b) as the arc semi-minor radius ("b") into Equation (7a) yields a somewhat complicated expression for radius of curvature at the observer along the given great elliptic arc. After much algebraic simplification we obtain

r   =   a (1 - e2 cos2 φ cos2 θ)3/2 / (1 - e2 [1- sin2 φ cos2 θ])1/2     (16a)

Equation (16a) is very well approximated by

r   ≈   a (1 + ½e2 [1 - cos2 θ(1 + 2 cos2 φ)] )     (16b),

having used (1 + x)^p ≈ 1 + px for |x| << 1 (p = 3/2 and 1/2), while neglecting terms in higher powers of e² << 1.

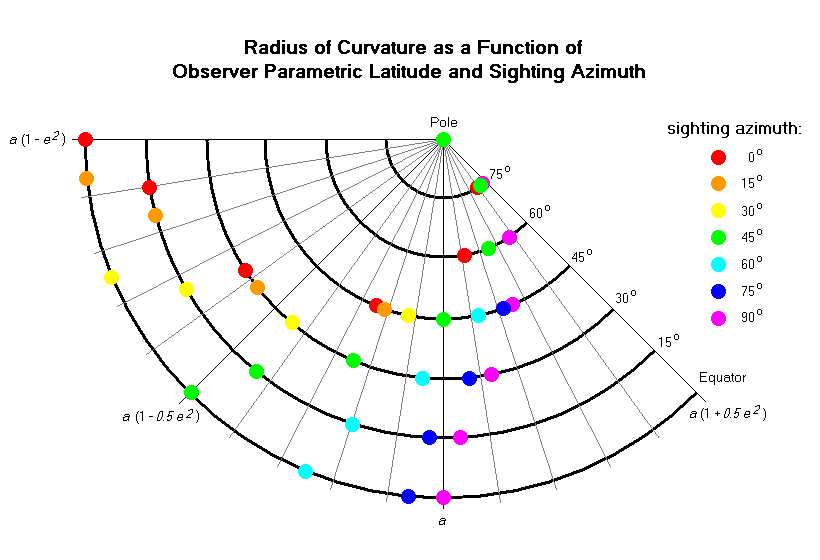
Figure 3 displays r based on Equation (16b) in 15° increments for both observer parametric latitudes and sighting angles. The graph's circular layout is motivated by this problem's geometry. The complete radius of curvature range for a given latitude is represented by a single set of circles from red (smallest radius) to violet circles (largest radius). That range diminishes from Equator to pole, corresponding to the cos² θ factor in Equation (16b).

Within any such range (i.e. for a given observer latitude), the 2 cos² φ factor in Equation (16b) changes in value quickest at φ = 45° (lime green circle), and least at either extreme (red and violet circles).⁷ At the poles where all sighting angles yield identical curvatures the colored circles converge and are respresented by a single color.

Figure 3

Equations (16a,b) reduce to certain special cases.
For a north-south observation angle (φ = 0°),

r   =   a (1 - e2 cos2 θ)3/2 / (1 - e2)½     (17a)

≈   a ( 1 + ½ e2 [1 - 3 cos2 θ] )       (17b)

which is identical to Equation (7c) on noting that parameter t is θ for meridians of longitude.

For an east-west observation angle (φ = 90°),

r   =   a / (1 - e2 sin2 θ)½     (18a)

≈   a (1 + ½ e2 sin2 θ )     (18b)

This radius of curvature is least at the Equator as simply a, Earth's equatorial radius.
The radius increases in value poleward, assuming there its maximal value of r ≈ a (1 + ½ e²).

At either pole the north-south and east-west formulae converge since all observation angles have the same radii of curvature.
Hence Equation (18b), derived for the east-west case, agrees with Equation (17b) for the north-south case.

6. An error is introduced in the length of arc o by applying spherical trigonometry to an ellipsoid.
    That error's order of magnitude is 1/e² radian. The entire range of arc lengths, from 0 to 90°
    contributes to radius of curvature with a correction term in 1/e². Hence the error wrought by
    Equations [10a,b] is on the order of 1/e⁴ and thus tolerable with the current prescription's accuracy.

Application - Horizon Distance and Hand Level Elevation Correction

Equations (16a,b) are applied by replacing Earth radius R_e in Equation (3b) for horizon distance and in Equation (1b) for hand level elevation correction by the radius of curvature r. We are not justified in considering Equations (1a) and (3a) because only the local radii of curvature at the observer have been obtained.

From Equation (3b) the observer's horizon distance is proportional to the square root of r. Thus a 1 part in 300 increase of r, relative to a spherical Earth model (r fixed at R_e) yields a roughly 1 part in 600 fractional rise in observable distance.

From Equation (1b) a hand level elevation correction is inversely proportional r itself. Thus a 1 part in 300 increase in r, relative to a spherical Earth model yields a decrease in elevation correction by 1 part in 300.

Reversal of sight angle by 180° does not change the radius of curvature; while reflection of the sight angle in the local meridian does not either. Collectively there results a 4-fold symmetry in radius of curvature at the observer as his sighting angle changes through the full circle. Thus sighting at 10° true provides an identical radius of curvature for 170°, 190° and 350°. This symmetry is implicit in the following discussion.

At the poles θ = 90° such that Equation (16b) indicates a maximal radius of curvature, an interesting result since it is there that the actual distance to Earth's center is least. The observable distance to one's horizon is larger than elsewhere; while the hand level elevation correction for a given sighting distance is smaller than elsewhere.

Aside from the poles, for a given observer latitude the radius of curvature is largest when sighting due east or west, and as seen by fixing cos θ in Equation (16b) and noting that east and west provide cos²φ = 0. The observable horizon is proportionately farther than for all other sighting angles; while the hand level elevation correction is least of all possible sighting angles.

The (signed) fractional change in horizon distance upon rotating one's sight angle from due north (or south) to due east (or west) is largest at the Equator at roughly (+) 1 part in 300. This fractional shift diminishes poleward, becoming (+) 1 part in 600 at 45° N (or S) and zero at the poles as all directions have the same radii of curvature there.

The (signed) fractional change in hand level elevation correction upon rotating one's sight angle from due north (or south) to due east (or west) is largest at the Equator at roughly (-) 1 part in 150. This fractional shift diminishes poleward, becoming (-) 1 part in 300 at 45° N (or S) and zero at the poles.

The fractional shifts in both horizon distance and hand level elevation correction are largest upon comparison of their values at either pole and when sighting due north or south at the Equator. This shift of 3/2 e² is roughly 1 part in 100 for elevation correction, and half of that for horizon distance.

Application - Global Mean Radius of Curvature

Equation (16b) is simple enough to provide a mean radius of curvature over the entire surface, with consideration of all possible observer latitudes and sighting angles. Importantly, r is not a function of the observer longitude. We thereby integrate r (θ, φ) noting that each latitudinal band carries a weight factor of cos θ to account for its area.⁸

Noting that only the terms proportional to ½ e² are not constant over the entire surface we denote the relevant double integrals I₁ and I₂,

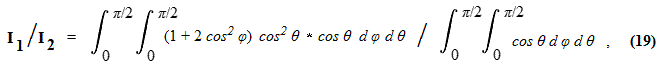the denominator providing normalization. These limits of integration leverage the problem's symmetry,
so considering just one hemisphere (north or south) and one quadrant of possible sighting angles.

The denominator double integral evaluates as π/2. The numerator requires, among other terms,
evaluating the integral of cos³ x dx, and results in 2π/3. Dividing by the denominator one has I₁ / I₂ = 4/3.

Substitution of this result into Equation (16b) yields

‹ r ›   =   a (1 - 1/6 e2)     (20)

where ‹ r › is the latitude and angle-averaged radius of curvature. Using e² ≈ 1/150, ‹ r › is 1 part in 900 less than the equatorial radius a.

Thereby when a spherical Earth model is employed the optimal (single) radius of curvature to use is given by Equation (20), roughly 4 ½ statute miles less than the equatorial radius a. Using the precise WGS84 ellipsoid parameters one obtains ‹ r › = 6371020.7 meters = 3958.77 statute miles and diminished (relative to a) one-third fraction of the difference between equatorial and polar radii.

The same distance arises when matching the volume of Earth, modeled as an oblate spheroid, to a sphere of equivalent volume. For the oblate spheroid volume V = 4/3 πa²b and for the sphere V = 4/3 πr³. Thus r = (a²b)^1/3, a quantity well approximated by Equation (20) recalling that b ≈ a (1 - ½ e²) and that the cube root of 1 - ½ e² is 1 - 1/6 e² for e² << 1.

What latitude yields a sighting angle-averaged radius of curvature matching the globally-averaged radius of curvature
given by Equation (20)? The sighting angle-averaged radius at a given latitude requires evaluation of

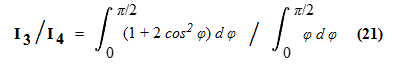where again the denominator normalizes.
I_3 / I_4 evaluates as π / (π/2) = 2, such that we obtain the equality

a (1 - 1/6 e2)   =   a ( 1 + ½ e2 [1 - 2 cos2 θ] )     (22)

where the left side is from Equation (20) and the right side from substitution of I₃ / I₄ in place of 1 + 2 cos² φ in Equation (16b). Solving, cos² θ = 2/3, θ = 35° 16'. Recalling that θ is the parametric latitude, use of Equation (8) yields the geographic latitude θ_g = 35° 21'.

This is also the latitude for which distance to Earth's center matches the radius of a sphere with equivalent volume to the oblate spheroid! In Equation (11b) the value cos² o = 1/3 matches r_min to the equi-volume sphere radius, a (1 - 1/6 e²). Noting that arc "o" in Equation (11b) is the co-latitude, when its cosine squared is 1/3 there is a concomitant squared sine of 1 - 1/3 = 2/3 and a squared sine of 1/3 for the latitude - which corresponds to the squared cosine of 2/3 in the solution of Equation (22).

Finally recall that the two extremal radii of curvature are at the poles and at the Equator when sighting due north or south. Their mean value is a (1 - ¼ e²), some 1 part in 600 less than a. Hence the fractional difference between this mean radius of curvature and the globally-averaged value of Equation (20) is e² /12, about 1 part in 1800.

8. The differential area element for integrating over the ellipsoid surface is r² (θ) cos θ d θ d ψ
    where ψ is the longitudinal coordinate. As r is a function of latitude θ it is an approximation to single out
    cos θ as sole contributor to the I₁ and I₂ integrands. Now r² varies by a fraction 1/e² from Equator to pole.
    Furthermore I₁ / I₂ contributes only to local radius of curvature via the terms in ½ e² of Equations (16a,b).
    Hence neglect of latitudinal dependence of r in I₁ and I₂ introduces an O(1/e⁴) error.

Application - Viewshed Area

Equations (3b,16b) specify the horizon distance for a given observer latitude θ and sighting angle φ, with the effective radius of curvature a from Equation (16b) replacing the fixed Earth radius R_e in Equation (3b). Therefore it should be possible to compute the observer's viewable area by integrating a function of this distance over all sighting angles.

For the area,

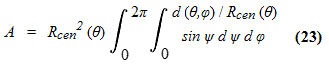where angular variable ψ ranges from 0 to the geocentric angle subtended by horizon distance as a function of latitude and sighting angle. d (θ, φ) is the horizon distance; while R_cen is the observer's distance to Earth's center.

Integration of Equation (23) requires evaluating the upper limit's cosine. Using the infinite series expansion of cos (d / R_cen) and noting that d << R_cen we discard higher order terms to obtain the very simple form

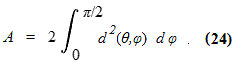We square both sides of Equation (3b) while using the effective radius of Equation (16b) in-place of R_e. Substitution of the resulting expression for d² into Equation (24) yields upon simplification

A   =   2πah ( 1 + ½ e2 [sin2 θ - cos2 θ] ).

(25a)9

The area is least at   the Equator with A roughly 1 part in 300 less     than 2πah.
The area is largest at either pole with A roughly 1 part in 300 greater than 2πah.

These fractional shifts agree with the fractional shifts in sighting angle-averaged horizon distance at either location. Noting Figure 3, for the Equator the mean fractional decrement in radius of curvature relative to a is ½ e², about 1 part in 300. From Equation (3b) this provides a 1 in 600 decrement in horizon distance. As the area of a near-circle is proportional to its radius squared, the 1 part in 300 decrement in area is recovered. The same argument applies to either pole albeit with replacement of "increment" for "decrement".

Equation (25a) suggests that for a spherical Earth

A   =   2πReh ,

(25b)

such that viewable area increases in direct proportion to height above the terrain, i.e. not as it's square root (as with horizon distance). Equation (25b) is trivally available by squaring both sides of Equation (3b) thence multiplying by π. Since 2πR_e is Earth's circumference, we have the remarkably simple and unobvious result that one's viewshed equals Earth's circumference multiplied by height above the terrain.

9. Equation (25a) may be rewritten as A   =   2πah (1 - ½ e² cos 2θ), having used the identity cos 2θ = cos² θ - sin² θ.

return to home page