Hand Levels for County Highpointing

Tips & Techniques for County Highpointing with Hand Levels ^*

Custom Search

^* by John Mitchler

Hand Levels
Hand levels are devices that allow you to determine a line of equal elevation (a line on a distant object that is of the same elevation as your eyeball). Basically, hand levels are tubes with a leveling bubble and a crosshair. One may use them to identify a single highpoint in gently rolling terrain and to determine which of several candidate areas is the highest. Hand levels may be found at survey supply stores, scientific stores, and rock hound shops. A cheap hand level can cost under $15 and most are more than $50. The best ones have magnification and scaling and cost $200. Some hand levels have no magnification and simply have a horizontal line (cross hair) with a level (spirit bubble). Magnification may be 2x or 5x.

Basic Use
To use the level, peer through the scope and notice three things: the distant terrain, the level bubble, and the centerline (crosshair). Line up the bubble with the centerline. Anything you see behind that line in the field of view is perfectly level with your eye. Common errors are to look right at the highpoint forgetting the bubble, or to forget that your eye is 5 feet above the ground. As Dave Covill says, "You need to make like Mitchler and get down and dirty." To be more accurate, lie on your belly so that your eyes are nearly the same elevation as the ground (but watch out for dung and cactus!). Out on the plains, a hand level is indispensable. On high peaks or where there is only one candidate for a highpoint, they are less necessary. One still gets use from it at other times, like on a long climb when one hand levels across a valley to the top of a peak of known elevation, to get an approximation of how far along we are. Of course, some multiple areas can't be evaluated because they are 1) too far apart, 2) cloaked by trees, or 3) too similar in elevation for hand levels to determine.

Multiple Areas
Hand levels are crucial for multiple area highpoints where the idea is to eliminate as many of the contour areas as possible, leaving only or two that are considered the highest. [Note: contour intervals of 20 ft or more are best suited for hand level analysis. In those situations, each closed contour area may have up to 19 feet of relief. That is certainly discernable by hand levels.] The trick in multiple areas is to systematically eliminate as many areas as possible, and the key to that is having a system of naming each area and a system of noting your field observations.

Here is one such system. Take the topo map and highlight each area and number them (before you head to the field). When you arrive at the multiple-area highpoint, hand level each area and write down notes on your topo such as "1 > 2" which means "area 1 is higher than area 2." If you write down "1 >> 2" then it means that area 1 is much higher than area 2. In that way, a highest candidate(s) will emerge. Walk over to it and sight to as many other areas as possible. This procedure may eliminate some areas as being too low and thus save future county highpointers time and effort.

Back Sighting
Back sighting usually confirms or conflicts with an original sighting. It is noteworthy how relative elevations appear different from different locations. Always back sight! If any areas seem similar in elevation, one should go over to those areas and back sight. For example, if on area 1 you had noted that "1 > 2" then you would walk over to area 2 and back sight. If confirmed, one would write down "2 < 1" which tells you that you went to area 2 and found it to be lower than area 1. Many times if area 1 appears to be about equal with area 2 at first sighting, by back sighting you can get a confirmation or conflict. If conflicting, write that down as well.

It's perfectly fine to discover two areas of equal elevation. Then that's a job for the laser surveyors! When you simply eyeball an area, you'll often find that your eyes can't be trusted. This has to do with the optical illusion of a false horizon, which frequently occurs when the land is slightly tilted, and you mistake it for being perfectly flat. Or your brain wants a higher horizon (that it is accustomed to having). To be higher than all other land is unusual and not seen in normal daily life.

Distances
Dave Covill relates, "I bought a roughly $30 hand level from a Sokkia store in Denver, a year after John Mitchler got his $15 plastic one [1995]. It was a bit nicer, but produced the same result generally. I lost it in 2000, and went back to the store and ended up buying a $75 one, with 2.5X magnification. It really makes a difference, as I can tell a 1-2 ft difference a half-mile away, whereas before I could perhaps determine a 4-7 ft difference, but nothing finer than that. At 100 yards, I can easily discern a 1 ft difference now. At a mile, it's probably good for 7-10 ft. Anything over that, and you need professional surveying equipment [and techniques]."

The basic idea that Dave describes is that magnification helps with distance. The David White True Sight basic hand level is accurate for 200 feet.

Earth Curvature and Measurement Error ^*

With increasing distance Earth's surface drops below the observer's horizontal plane, introducing a correction term which must be accounted for.
This term's magnitude rises as the distance squared,

correction (feet) = 0.67 x distance² (miles) [1].

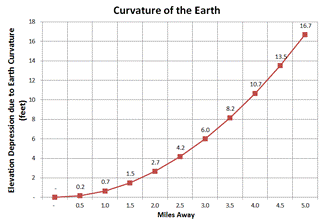
Thus at one mile an object 8 inches higher than the sight leveler appears to be at the same elevation.
Similarly, at one-half mile an object at his elevation appears to be 2 inches lower.

This correction term is smaller than multiple measurement error sources, which include yet are not limited to

Atmospheric refraction
User misinterpretation of bubble location
Instrument precision

Equation [1] is valid only for the short distances encountered with hand-leveling. For larger observer to horizon distances (such as encountered with high altitude aircraft and satellites) a more robust formula is required. This calculator provides valid results for all observer to object distances out to the theoretical maximum of one-quarter Earth's circumference (some 6,218 miles).

Type an observation distance in the left textfield, in miles, to calculate the corresponding elevation correction in feet.

The geometric apparatus for computing a hand level elevation correction may equally be used to determine the distance to one's horizon when elevated a given amount above an otherwise featureless plain. In other words, how far can one see when atop a mountain with 4,000 feet of vertical relief?

For small vertical relief as encountered in the mountains ("small" being relative to Earth's radius) we have the approximate relation

distance to horizon (miles) = 38.7 x square root (height) [2],

the height being in thousands of feet. Thus on a perfectly clear day the horizon is some 75-80 miles distant while atop a mountain 4,000 feet above the surrounding terrain.

This calculator provides valid results for all observer heights out to infinity, whence the visible horizon
is one-quarter Earth's circumference distant as measured along the surface.

Type an elevation in the left textfield, in feet, to calculate the corresponding horizon distance in miles (as measured along the ground).

There are minor errors introduced by having modeled the Earth as a sphere rather than an oblate spheroid.
A mathematical treatment of these considerations is now available.

^* This section's concept was first described and promoted by Dave Covill, Scott Surgent and Bob Packard.
Adam Helman wrote the section, providing an alternative formulation of the distance/elevation correction
relationship which is more transparent and mathematically robust than the original prescription.
The graph is by Dave Covill. The calculators are by Adam Helman.

Care of your Level
Remember to write or scratch your name and phone number on the level. Most levels come with a leather case, stiff and bulky.

Dave Covill suggests, "Ask instead for a foam case, smaller but easier to fit it into, and easier to stuff in my pocket." For my David White True Sight model, I bought a soft eyeglass case at REI and it fits perfectly. The cheaper models are open-ended and may fill with dust, although I've managed to keep mine clean. The more expensive models are airtight. I do not believe that any require calibration.

Alternatives
Dave Covill reminded me that a Silva Ranger (or similar $40) compass has an inclinometer built in it, which, if set to zero degrees, can function as a crude hand level. You sight across the top edge of the compass, while your partner tells you to move it up or down nike shox navina to make the little plastic arrow inside point to zero. Whatever you sight to along that top edge, is elevationally even with you. It's probably good for 20 feet over a half mile.

The same concept can be used with a water bottle or U-shaped tube filled with water. The idea is to establish a perfectly level plane and you do that by leveling your eye with the level plane of water in a bottle or the two tubes with water. Obviously, there are more sophisticated tools that make use of lasers, but that's left for more hard core county highpointers.

Brands
If you web search on hand levels, you may run across carpenter levels. Try to distinguish between hand sight levels used for surveying.

If you are interested in owning a hand level, be it 1X, 2X, 5X, etc.., contact Surveyors Exchange in Anchorage, Alaska and ask for Donna Wilmarth, mentioning your connection to the county highpointers.

As you probably need to have one shipped from "somewhere", it may as well be from Alaska!

Surveyors Exchange
3695 Springer Street
Anchorage, Alaska 99503
telephone 907-561-6501
Sokkia of Olathe, Kansas offers some nice models (tel.1-800-476-5542). David White of Germantown, Wisconsin offers several different models (tel.1-800-732-5478).

On-line stores offer many different brands at many different prices and can usually offer bulk discounts). Try www.mytoolstore.com here (tel.1-800-347-5096) or www.ascscientific.com here.

back to FAQs and Rules page